補足円筒絞りの塑性力学解析ダイR部の計算

カテゴリー：絞り加工

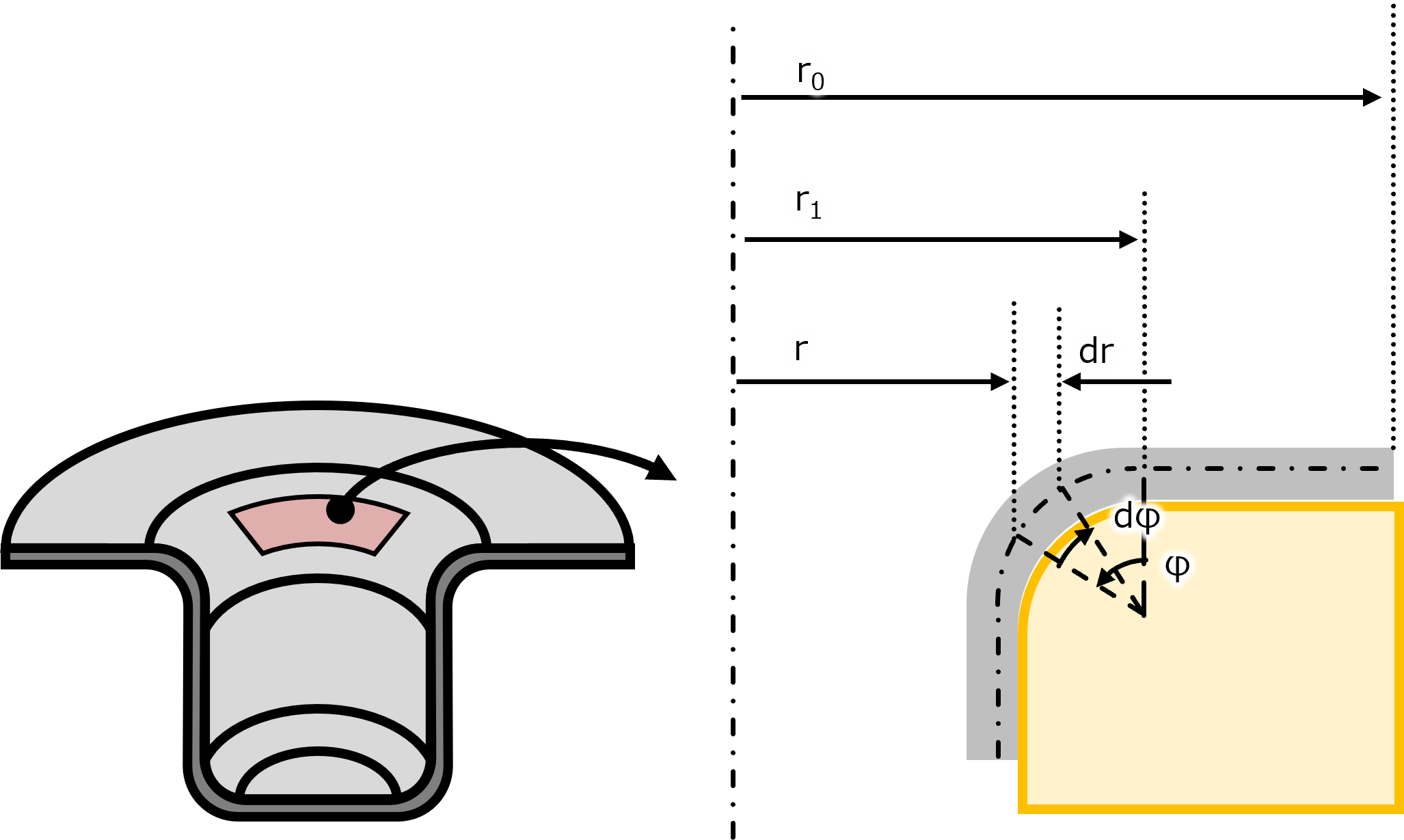
本ページではダイRを対象に計算方法を解説する。
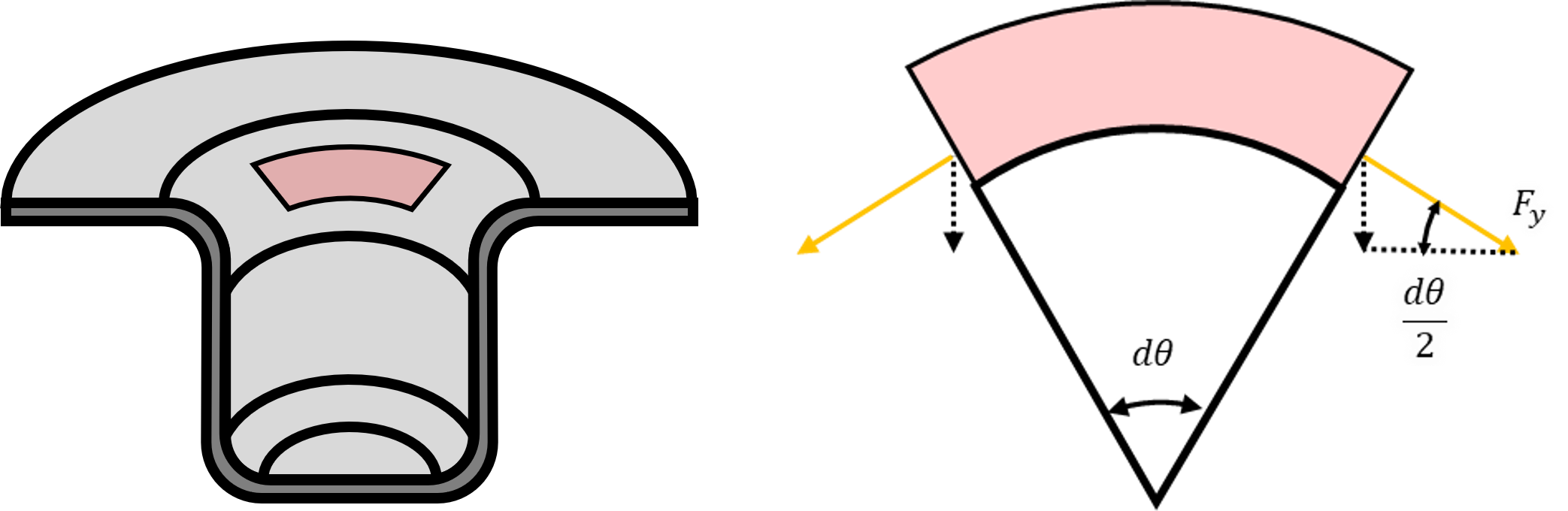
上左図の要素の断面図が上右図である。円周方向の角度Θだけでなく、ダイＲ上の角度φも関わるため、フランジ部の計算より複雑になる。そのため、本ページでは板厚変化だけでなく摩擦力の影響を無視して計算を行う。また、ダイRは曲げ応力も発生するが併せて無視する。

以下の手順で計算する。
まず微小要素の各面にかかる荷重を計算を行う。
そこから、子午線方向と板厚方向それぞれの力の釣り合いを計算する。
そこから求めた式を積分する。その際、境界条件（フランジ部の応力）から、子午線方向と半径方向の応力を求める。

微小要素の各面にかかる荷重

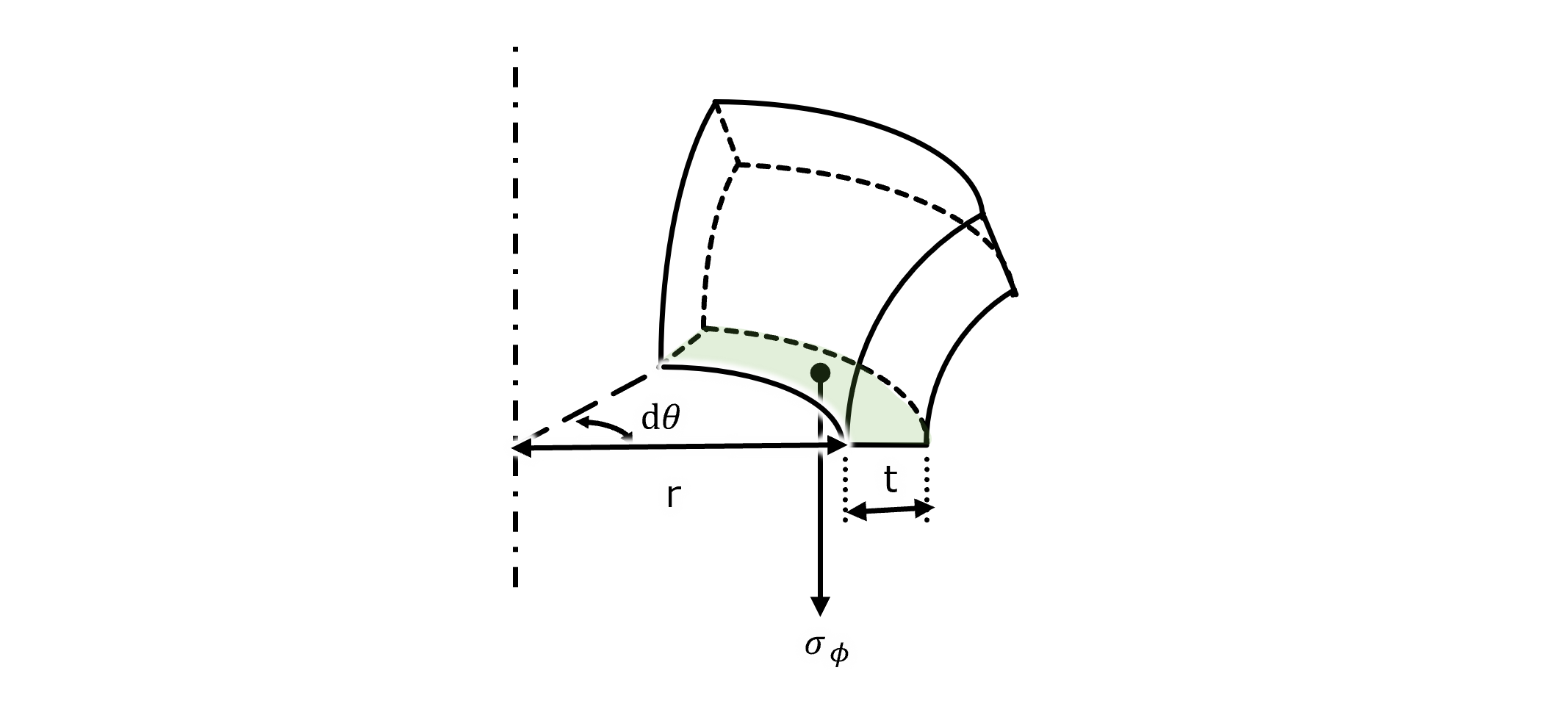
子午線方向の応力をσ_φとする。緑の面の荷重をF_gとする。面積はtrdΘなので

\[ F_g=\sigma_\phi trd\theta \]

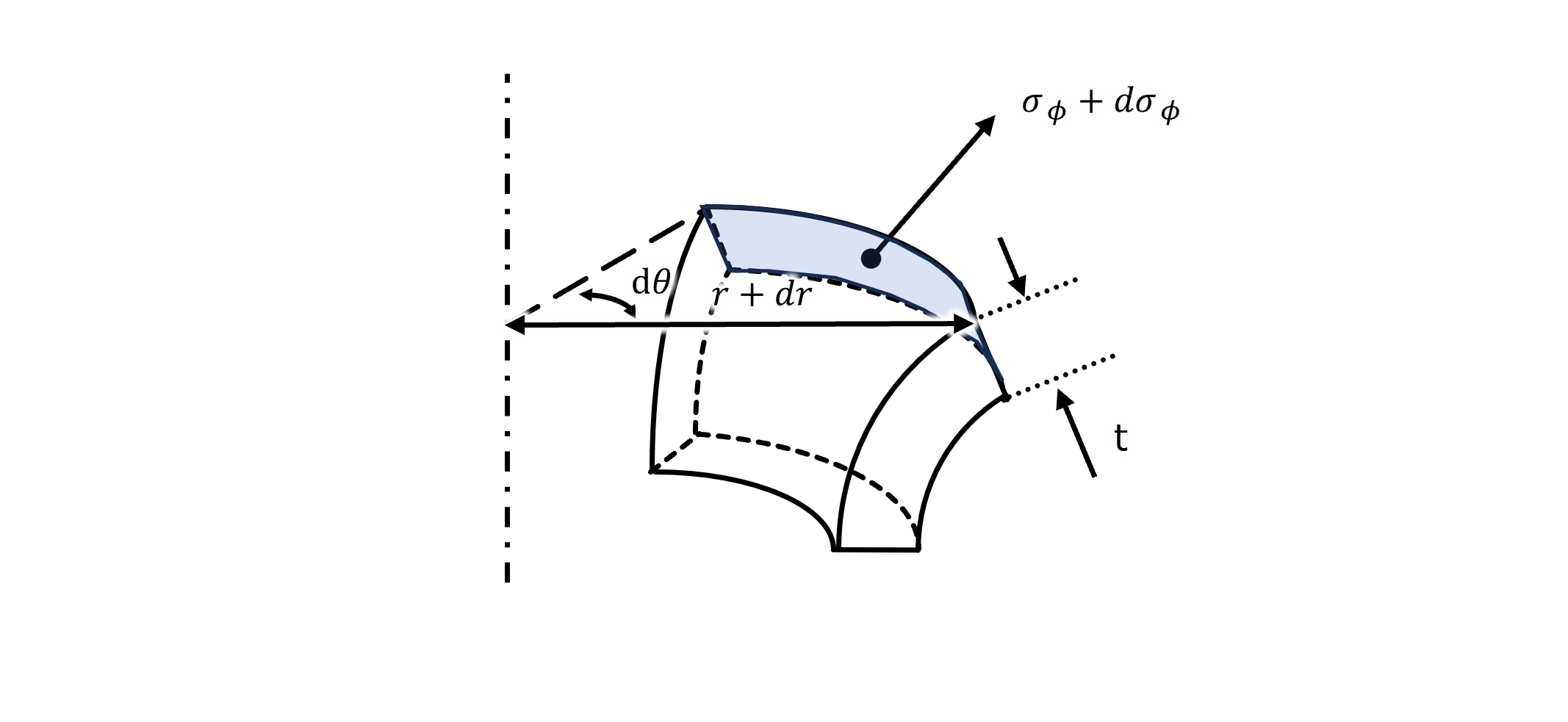
次に青面にかかる力F_bを計算する。上記同様に計算して、下式のようになる。

\[ F_b=(\sigma_\phi+d\sigma_\phi)(r+dr)td\theta \]

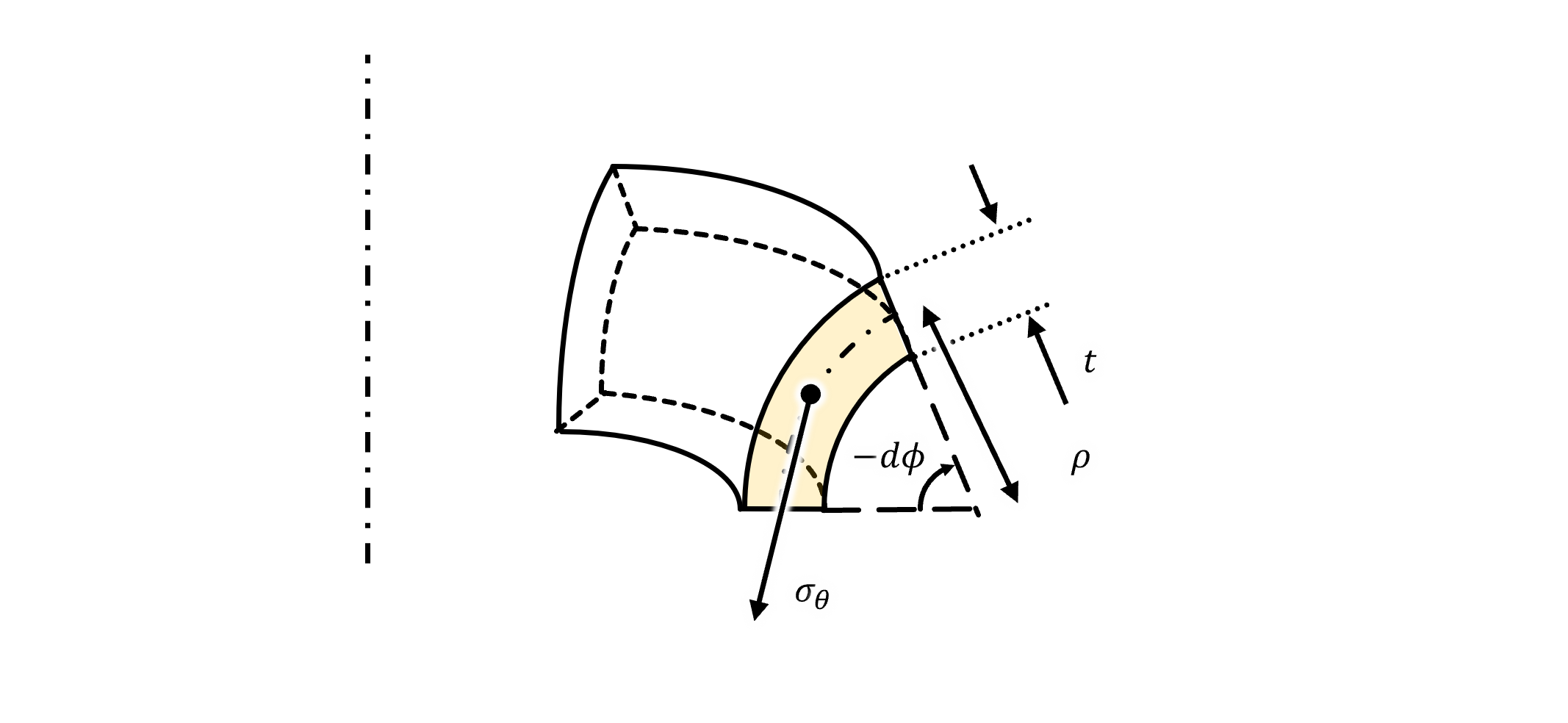
黄色の面の荷重をF_yとする。ダイRの原点から板厚の中立面までの距離をρとする。（ρ=rd+t)
面積はtρ(-dφ)tなので

\[ F_y=\sigma_\theta t\rho(-d\phi) \]

なお、φは反時計回りを正としており、この微小要素の角度は時計回りに取っているため-dφである。

微小要素にかかる力のつりあい

断面から子午線方向の力を考えると

\[ 2F_y sin\frac{d\theta}{2}\approx F_y sind\theta \]

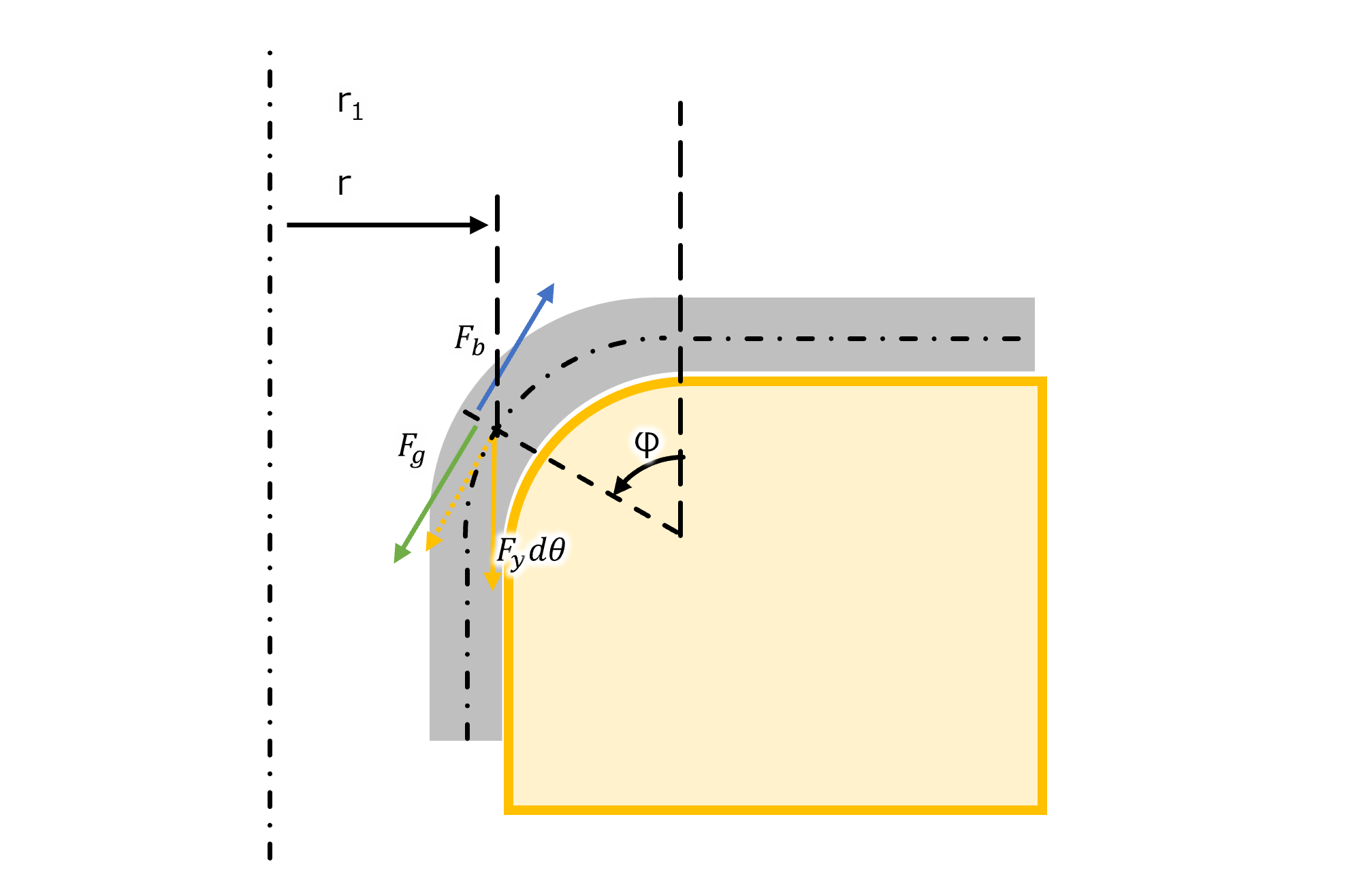
F_g,F_b, F_yの力の釣り合いをとると、

\[ F_g+F_y d\theta cos\phi=F_b \]

この式に、上で求めた式を代入して

\[ \sigma_\phi rtd\theta+\sigma_\theta \rho t(-d\phi)d\theta cos\phi=(\sigma_\phi+d\sigma_\phi)(r+dr)td\theta \]

t,𝑑𝜃を消去かつ drdθ≈0として整理すると

\[ \sigma_\theta \rho (-d\phi) cos\phi=\sigma_\phi dr +rd\sigma_\phi \]

幾何学的に以下の式が成立する

\[ r=r_1-\rho sin\phi \]

微分して、左右の項を入れ替えて

\[ \rho cos\phi=-\frac {dr}{d\phi} \]

これを代入して

\[ \sigma_\theta (-d\phi) (-\frac {dr}{d\phi} )=\sigma_\phi dr +rd\sigma_\phi \]

rdrで割って、整理すると

\[ \sigma_\theta d=\sigma_\phi dr+rd\sigma_\phi \] \[ \frac{d\sigma_\phi}{dr}+\frac{\sigma_\phi+\sigma_\theta}{r} =0 \phantom{zzzz}(1)\]

φを𝑟に置き換えると、フランジ部と同一式であり、半径方向の応力がそのまま子午線方向に変わったことがわかる。

σ_φ,σ_θの算出

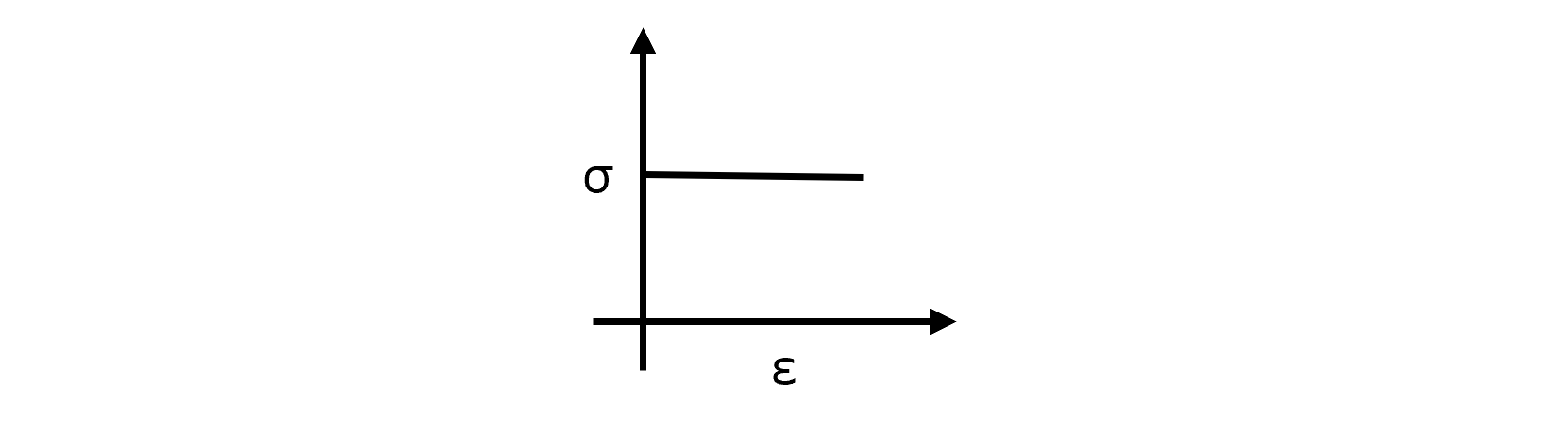
以下の計算はフランジ部と同一である。ブランク材は剛完塑性体とする（上図の応力ひずみ線図のように、弾性変形がなく、また加工硬化もない）また、ブランク材はトレスカの降伏条件に従うとする。フランジ内部の材料要素には板厚方向の応力が作用しない、かつ、\[\sigma_{\theta} \lt 0 \leq \sigma_{\phi}\]である。

トレスカの降伏条件より

\[ \frac{\sigma_{max} - \sigma_{min}}{2}=\frac{\sigma_Y}{2} \]

つまり

\[ \sigma_{\phi}-\sigma_{\theta}=\sigma_Y \]

なおσ_Yは降伏応力である。これを上で求めた(1)式に代入すると

\[ \frac{d\sigma_{\phi} }{dr}=-\frac{\sigma_Y}{r} \]

これを積分する

\[ \int \frac{d\sigma_\phi}{dr} \, dr = -\sigma_Y \int \frac{1}{r} \, dr \] \[ \sigma_{\phi}=-\sigma_Ylnr+C_1 \]

ダイス肩r=r₁における応力σ_φは、フランジ部r=r₁のσ_rに等しい。摩擦の影響を無視する（μ=0）時、半径方向の応力σ_r1は

\[ \sigma_{r1}=\sigma_Y\ln\frac{r_0}{r_1} \]

である。よって

\[-\sigma_Y lnr_1+C_1 =\sigma_Y\ln\frac{r_0}{r_1} \]

\[C_1 =\sigma_Y lnr_0 \]

つまり

\[ \sigma_\phi=\sigma_Y\ln\frac{r_0}{r} \]

が成立する。

\[ \sigma_{r}-\sigma_{\theta}=\sigma_Y \]

なので

\[ \sigma_\theta=-\sigma_Y\ln(1-\frac{r_0}{r}) \]

参考文献

日本塑性加工学会編、わかりやすいプレス加工、日刊工業新聞社（2000）

益田森治、室田忠雄、工業塑性力学、養賢堂（1980）

微小要素の各面にかかる荷重

微小要素にかかる力のつりあい

σφ,σθの算出

参考文献

σ_φ,σ_θの算出