補足円筒絞りの塑性力学解析フランジ部の計算

カテゴリー：絞り加工

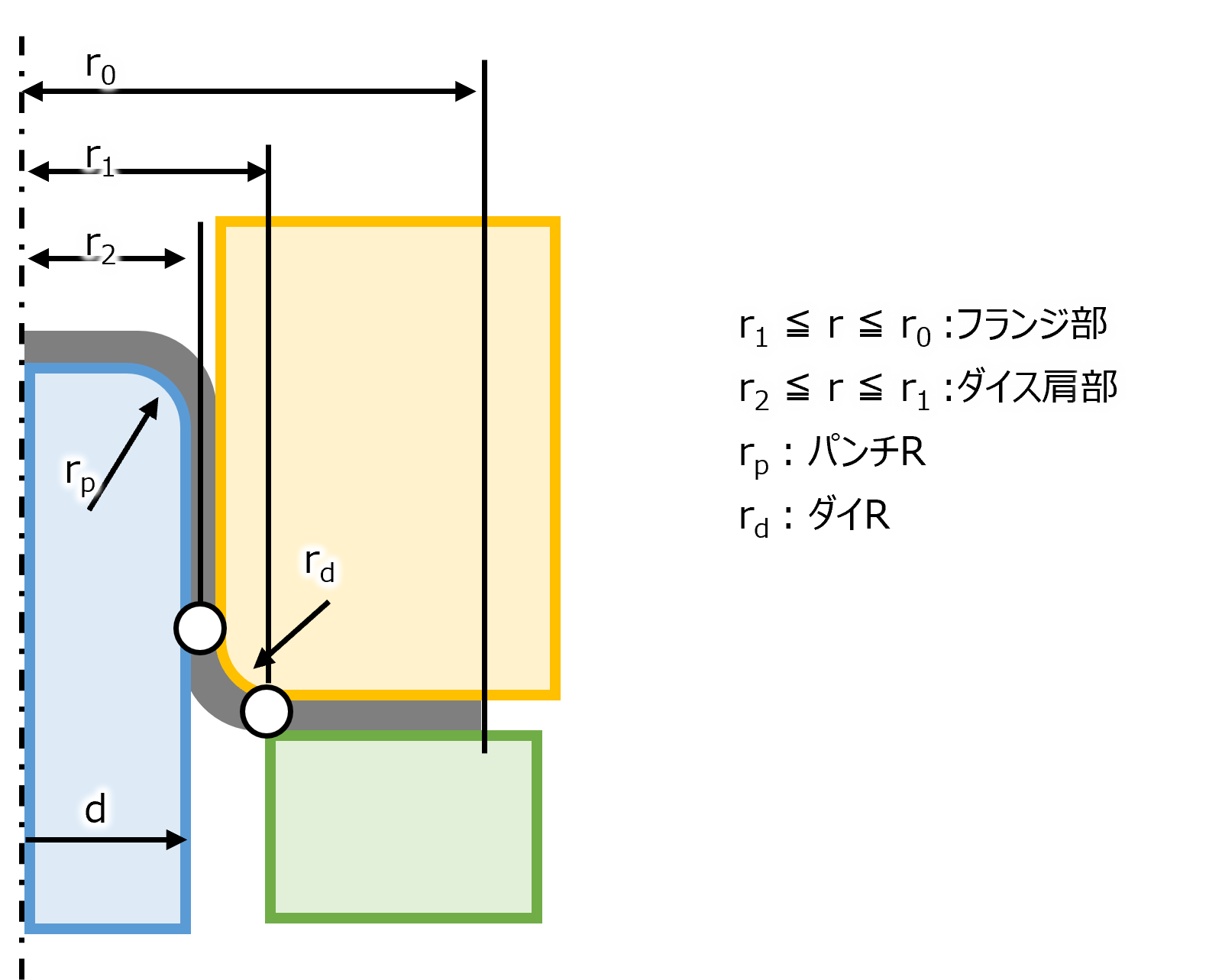
本ページではフランジ部を対象とした計算方法を解説する。上図は再掲ではあるが、記号は以下の様に定義する。まずは切り出した要素の各面にかかる荷重を計算を行う。そこから、半径方向と板厚方向それぞれの力の釣り合いを計算する。そこから求めた式を積分し、境界条件から半径方向と半径方向の応力を求める。

微小要素の各面にかかる荷重

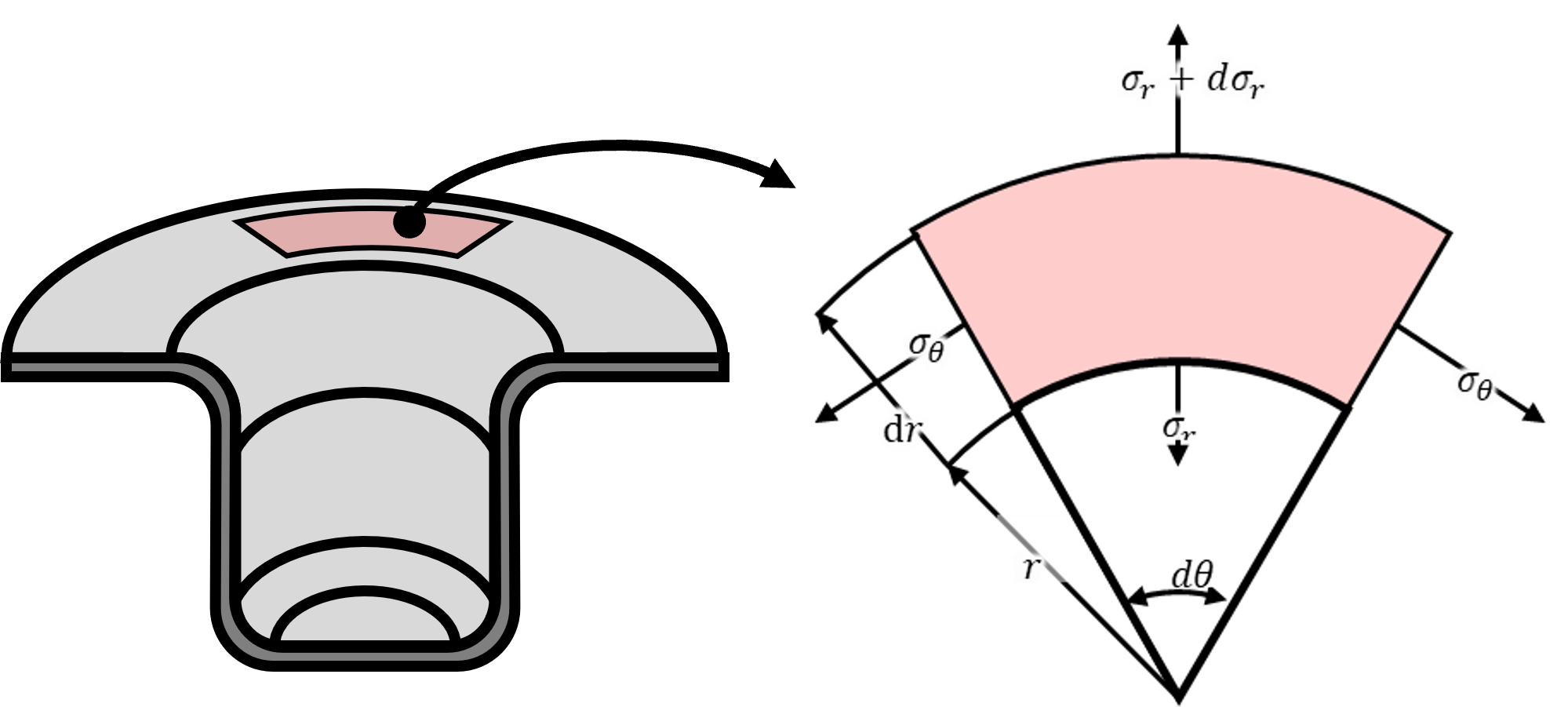
フランジの材料要素の一部を切り出したのが上右図である。フランジ部はパンチによる絞り成形によって引き込まれるため、円周方向に圧縮応力σ𝜃が発生する。（図はσ_θを正の方向で書いているが、実際には圧縮応力であるので、マイナスである。）そしてσ_θと釣り合うために円周の法線方向に引張応力σ_rが発生する。以下の計算では簡素化のため板厚一定として行う。

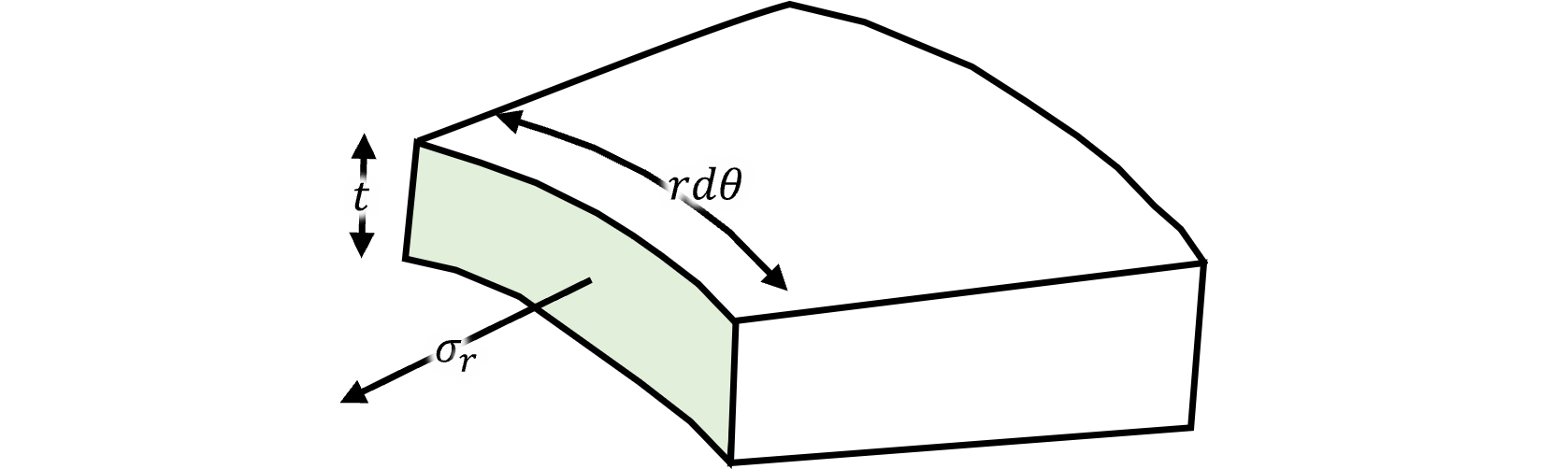
まずは緑面にかかる力F_gを計算する。応力×面積を求めればよいので以下の式になる。

\[ F_g=\sigma_r rtd\theta \]

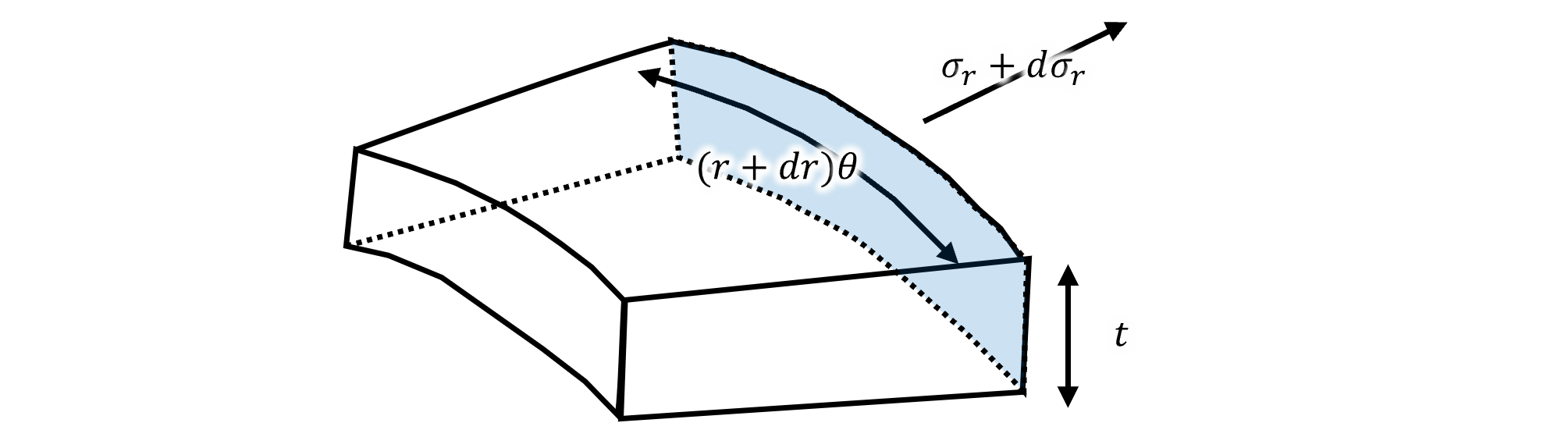
次に青面にかかる力F_bを計算する。上記同様に計算して、下式のようになる。

\[ F_g=(\sigma_r+d\sigma_r)(r+dr)td\theta \]

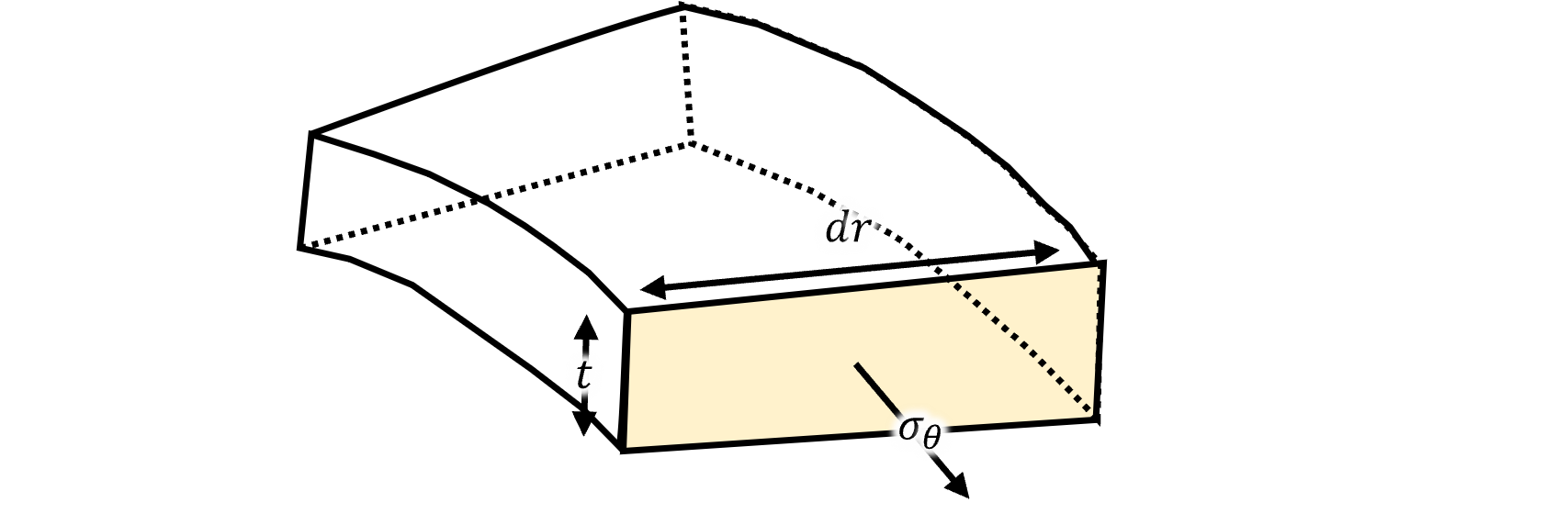
最後に黄面にかかる力Ｆ_yを計算する。

\[ F_y=\sigma_\theta tdr \]

微小要素にかかる力のつりあい

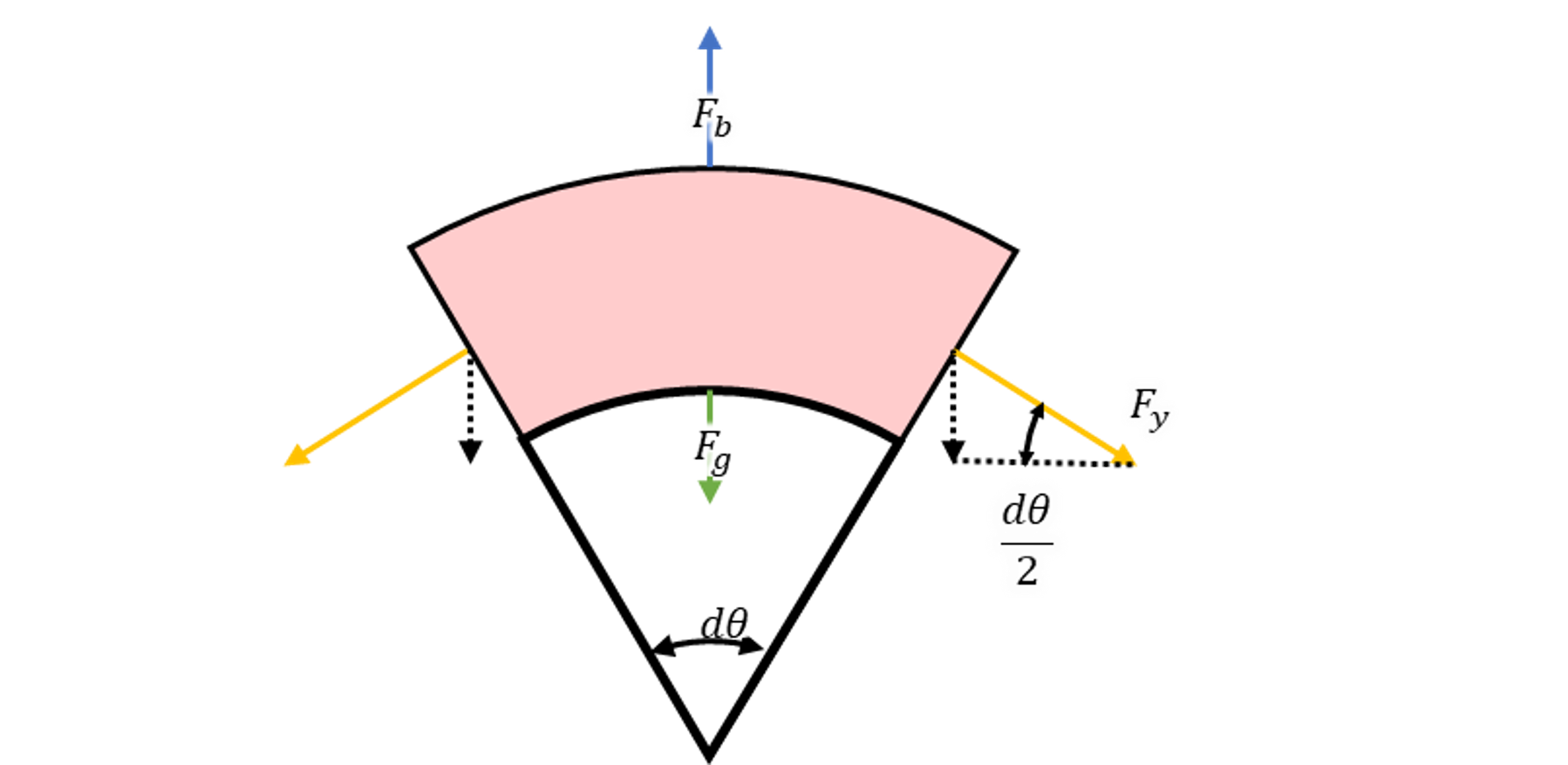
F_g,F_b, F_yの力の釣り合いをとると、

\[ F_g+2F_y sin\frac{d\theta}{2}=F_b \]

dθは微小なので以下の近似が成立する。

\[ sin\frac{d\theta}{2}\approx\frac{d\theta}{2} \]

そのため、上のつりあいの式は以下の様に式変形できる。

\[ F_g+F_y d\theta=F_b \]

この式に、上で求めた式を代入して

\[ \sigma_r rtd\theta+\sigma_\theta tdrd\theta=(\sigma_r+d\sigma_r)(r+dr)td\theta \]

t,𝑑𝜃を消去かつ drdθ≈0として整理すると

\[ \sigma_\theta dr=\sigma_rdr+rd\sigma_r \] \[ \frac{d\sigma_r}{dr}+\frac{\sigma_r+\sigma_\theta}{r} =0 \phantom{zzzz}(1)\]

σ_r,σ_θの算出

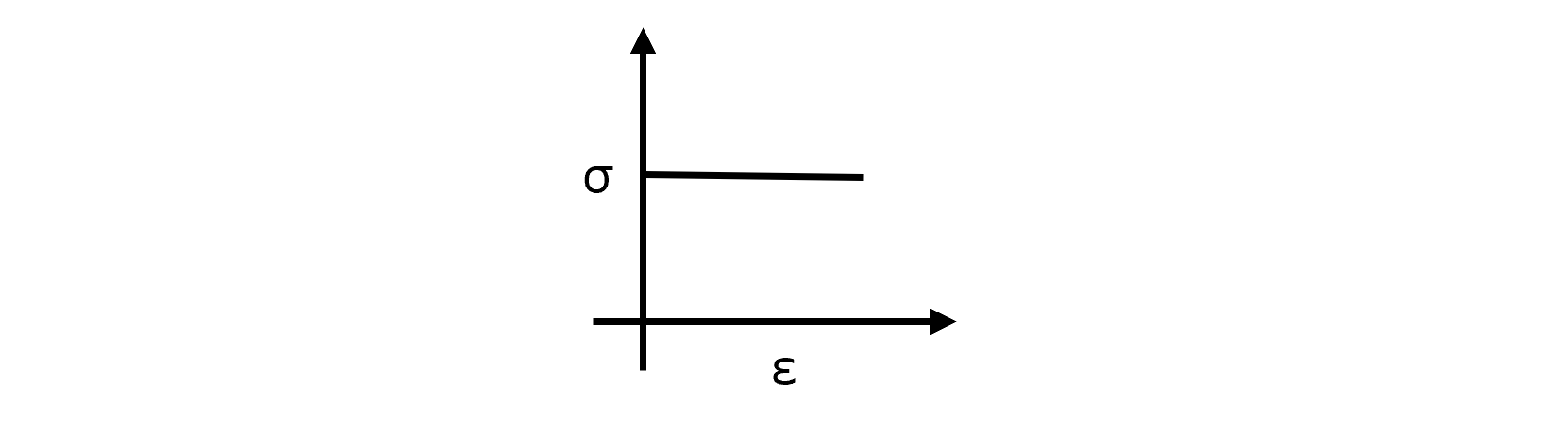
ブランク材は剛完塑性体とする（上図の応力ひずみ線図のように、弾性変形がなく、また加工硬化もない）また、ブランク材はトレスカの降伏条件に従うとする。フランジ内部の材料要素には板厚方向の応力が作用しない、かつ、\[\sigma_{\theta} \lt 0 \leq \sigma_{r}\]である。

トレスカの降伏条件より

\[ \frac{\sigma_{max} - \sigma_{min}}{2}=\frac{\sigma_Y}{2} \]

つまり

\[ \sigma_{r}-\sigma_{\theta}=\sigma_Y \]

なおσ_Yは降伏応力である。これを上で求めた(1)式に代入すると

\[ \frac{d\sigma_{r} }{dr}=-\frac{\sigma_Y}{r} \]

これを積分する

\[ \int \frac{d\sigma_r}{dr} \, dr = -\sigma_Y \int \frac{1}{r} \, dr \] \[ \sigma_{r}=-\sigma_Y lnr+C_0 \]

ブランク材の外縁である𝑟=r₀に摩擦力σ_r=σ_Fがかかるとすると (実際、外縁がわずかに厚くなる)

\[C_0=\sigma_F+\sigma_Y lnr_0 \]

つまり

\[ \sigma_r=\sigma_Y\ln\frac{r_0}{r}+\sigma_F \]

\[ \sigma_{r}-\sigma_{\theta}=\sigma_Y \]

であるから

\[ \sigma_\theta=-\sigma_Y\ln(1-\frac{r_0}{r})+\sigma_F \]

参考文献

日本塑性加工学会編、わかりやすいプレス加工、日刊工業新聞社（2000）

益田森治、室田忠雄、工業塑性力学、養賢堂（1980）

微小要素の各面にかかる荷重

微小要素にかかる力のつりあい

σr,σθの算出

参考文献

σ_r,σ_θの算出