均等曲げのスプリングバック解析①｜均等曲げの計算

カテゴリー：曲げ加工、寸法精度不具合

曲げはV曲げやL曲げなどを代表として、様々な曲げの形態があることを解説してきた。
V曲げやL曲げのように、曲げモーメントが部位によって変化する曲げを不均等曲げと呼ぶ。
本ページでは、曲げモーメントが部位によって変化しない均等曲げを取り扱う。
この均等曲げの計算式を踏まえ、次ページでスプリングバック量の計算を行う。
スプリングバック量の計算内容を先に知りたい場合、以下の記事参照のこと。

スプリングバック量の解説記事を読む

計算の前提

①板の中立面のひずみは０である
②板厚方向の応力は無視
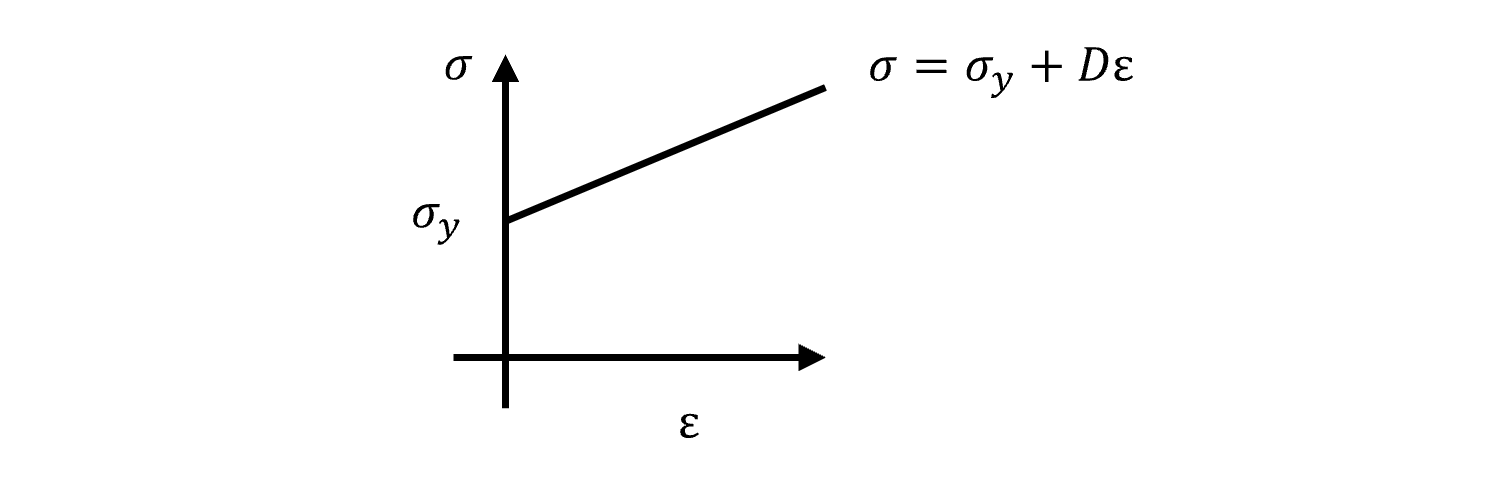
③材料は弾性変形を無視した剛塑性体とし、以下の図に示す直線硬化式が成立する
なお、σ_yはで降伏点、Dは加工硬化の程度を示す傾きである。

均等曲げの計算｜応力の計算

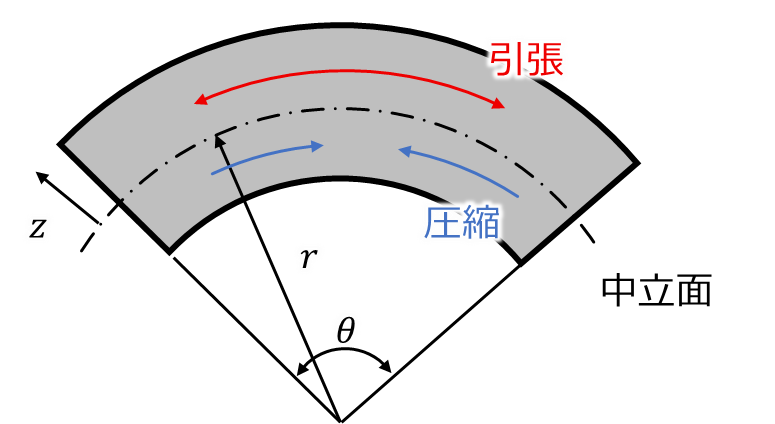
均一な曲げモーメントMによって、中立面の半径rに板を曲げたとする。この時、中立面から半径方向の距離をzとする。このときひずみεは以下の式のようになる。

\[ \varepsilon = \frac{(r+z)\theta - r\theta}{r\theta} = \frac{z}{r} \]

応力は以下の式で示すことができる

\[ \sigma = \sigma_y + D\varepsilon \]

そのため、ひずみは以下の様に式変形できる

\[ \sigma = \pm \sigma_y + D\frac{z}{r} \]

なお、引張領域>0で+σ_yはあり、圧縮領域z<0で-σ_yである。

均等曲げの計算｜塑性域の曲げモーメントの計算

単位幅当たりのモーメントは

\[ M = \displaystyle \int_{0}^{\frac{t}{2}} \sigma z dz = \displaystyle \int_{0}^{\frac{t}{2}} (\sigma_y z + D\frac{z^2}{r} )dz \]

\[ M =\left[ \frac{\sigma_y z^2}{2} + \frac{Dz^3}{3r} \right]_0^\frac{t}{2} \]

\[ M = \frac{1}{4}\sigma_y t^2 + \frac{Dt^3}{12r} \]

平均変形抵抗をσ_mとし、以下の式で表す。

\[ \sigma_m = \sigma_y + \frac{Dt}{3r} \]

σ_mを用いるとMは以下の式で示せる。

\[ M=\frac{\sigma_m t^2}{4} \]

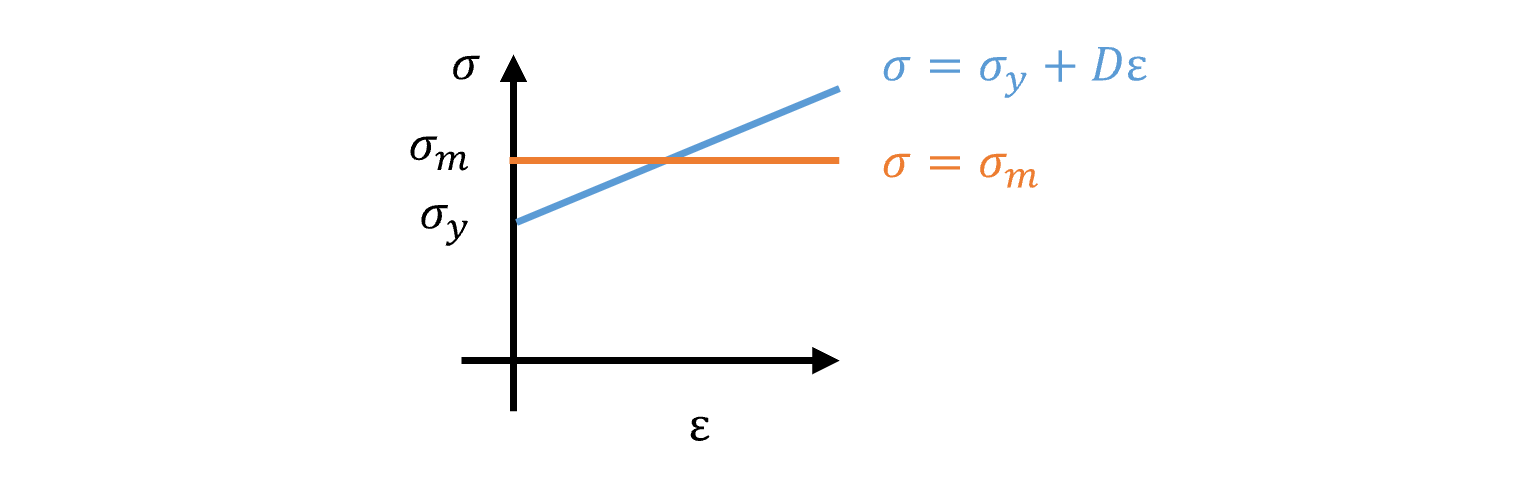
均等曲げの時のモーメントを算出することができた。

均等曲げの計算｜弾性域の曲げモーメントの計算

今までの説明で塑性域でのモーメント計算を行ってきたが、この節では弾性域の計算を行う。
詳細は次ページで述べるが、スプリングバック量の計算に弾性域の曲げモーメントが必要になるからである。
なお、弾性域はフックの法則である以下の式が成立する。

\[ \sigma=E\varepsilon \]

Eはヤング率である。
これを用いて曲げモーメントを計算する。

\[ M = \displaystyle \int_{0}^{\frac{t}{2}} \sigma z dz = \displaystyle \int_{0}^{\frac{t}{2}} E\frac{z^2}{r} dz \]

\[ M =\left[ \frac{Ez^3}{3r} \right]_0^\frac{t}{2} \]

\[ M = \frac{1}{12r} Et^3 \]

\[ M = \frac{1}{4}\sigma_y t^2 + \frac{Dt^3}{12r} \]

ここで、断面二次モーメントIは以下の示せる。

\[ I = \frac{1}{12}bh^3\]

b=1,h=tを代入すると

\[ I = \frac{1}{12}t^3\]

となる。
これで上式を置き換えると

\[ M = \frac{EI}{r}\]

まとめ

本ページでは、塑性域と弾性域それぞれの曲げモーメントを計算した。
弾性域の曲げモーメントは

\[ M = \frac{1}{4}\sigma_y t^2 + \frac{Dt^3}{12r} \]

塑性域の曲げモーメントは

\[ M=\frac{\sigma_m t^2}{4} \]

つまり曲げモーメントは弾性域では板厚の3乗で効いたのに対し、塑性域では板厚の2乗しか効かないことがわかる。

参考文献

日本塑性加工学会編、わかりやすいプレス加工、日刊工業新聞社

吉田総仁、弾塑性力学の基礎、共立出版株式会社 (1997)