均等曲げのスプリングバック解析②|スプリングバック量の計算
カテゴリー:曲げ加工、寸法精度不具合
本ページでは均等曲げのスプリングバックの計算を解説する。
スプリングバック量の計算にあたって、事前知識として必要な均等曲げについては以下のページで解説した。
必要であれば以下の記事を参照のこと。
スプリングバック量の計算手順
スプリングバックの計算手順を説明する。
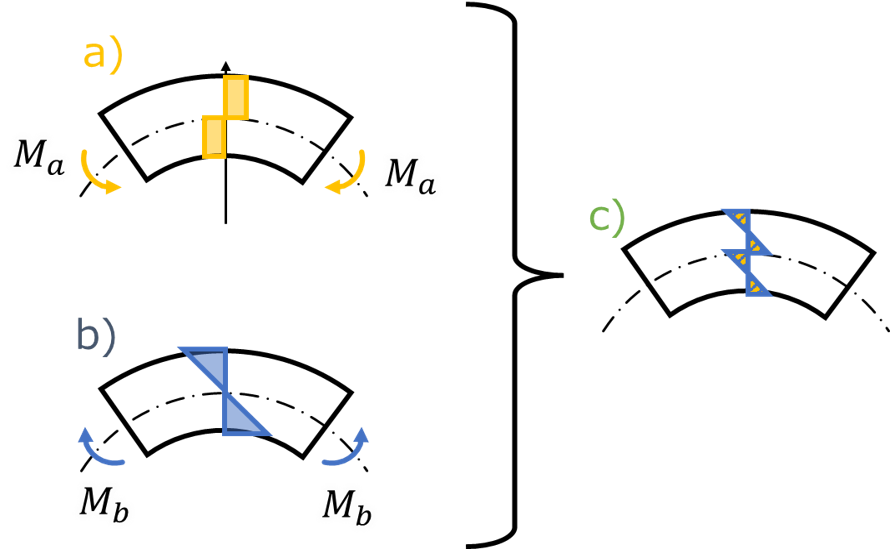
スプリングバック後は荷重の除荷後応力がつり合ってモーメントが発生していない状態である。
そのため、
a)均等曲げのモーメントMaに、
b)スプリングバックによるモーメントMbを、
c)足し合わせモーメントが0になればよい。
これを図解したのが下図である。
a)の時点と、c)の時点の角度の差がスプリングバック量になるため、これを求めにいく。
スプリングバック量の計算
これからスプリングバック量の計算を行う。数式の計算が多いため、スプリングバック量の式のみ知りたい場合、次の節までスクロールしてください。
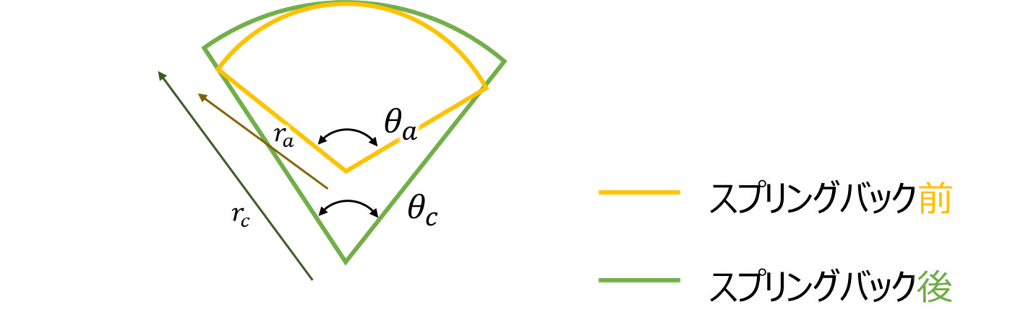
スプリングバック前の半径をra 角度をθa、スプリングバック後の半径をrc 角度をθcとする。
スプリングバックは弾性回復による減少であるから、弾性変形とみなせる。
弾性域の曲げモーメントは以下の式で示せる。(計算式は均等曲げの解説記事参照のこと)
スプリングバックによる曲率の変化量をΔ(1/r)とすると
なおΔ(1/r)は以下の式である。
またスプリングバック量Δθは以下の式である。
スプリングバック前後で材料長は変化しないので以下の式が成立する
これを式変形して
上のモーメントの式に代入して
両辺にraθaをかけて、左右の項を入れ替えると
均等曲げのモーメントMaとスプリングバックによるモーメントMbは、足し合わせるとモーメントが0になるので
つまりスプリングバックの変化量は
均等曲げの解説記事で以下の式が成立することを示した。なおσmは平均変形抵抗であり、降伏応力に相関する値である。
そのため、スプリングバック量は以下の式で示すこともできる。
スプリングバック量に影響する因子
スプリングバック量は以下の式で示せることがわかった。
この式から、スプリングバック量を減らすためには
・材料強度を下げる
・曲げRを小さくする
・曲げ角度を小さくする
・ヤング率の大きい材料を用いる
・板厚をあげる
・曲げモーメントを減らす
・断面二次モーメントをあげる
ことが有効であることがわかる。
これらは実際に有効であることが過去の先行研究からも明らかである。
また別のページでこれら因子の効果を説明する。
まとめ
本ページでは、スプリングバック量の計算式を明らかにした。 またその式から、スプリングバック量に影響する因子を明らかにした。