円筒絞りの塑性力学解析

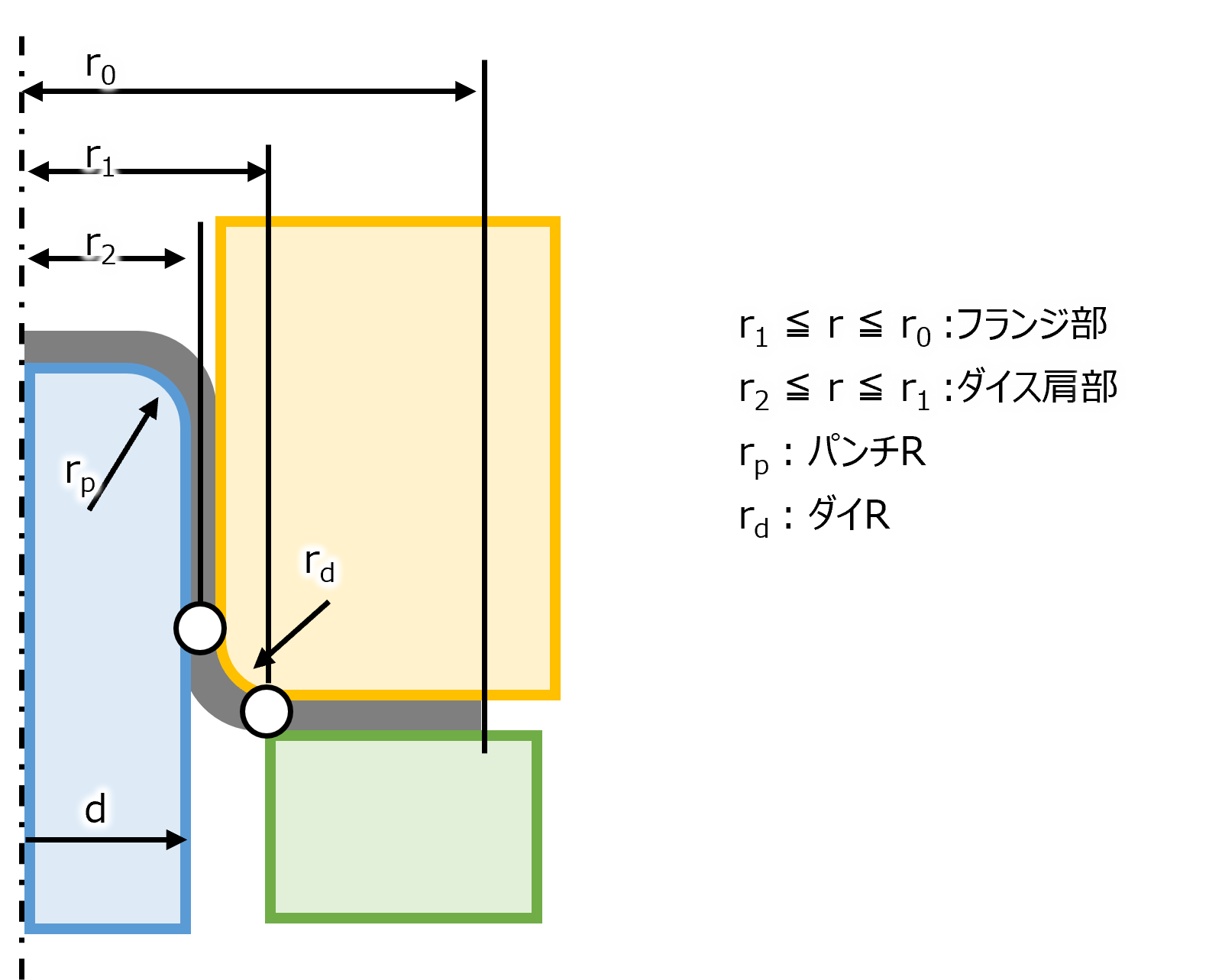
本節では円筒絞りの塑性力学解析について解説していく。 フランジ部⇒ダイR部⇒側壁部（パンチRとダイRを結ぶところ）の順で解説する。

フランジ部の計算

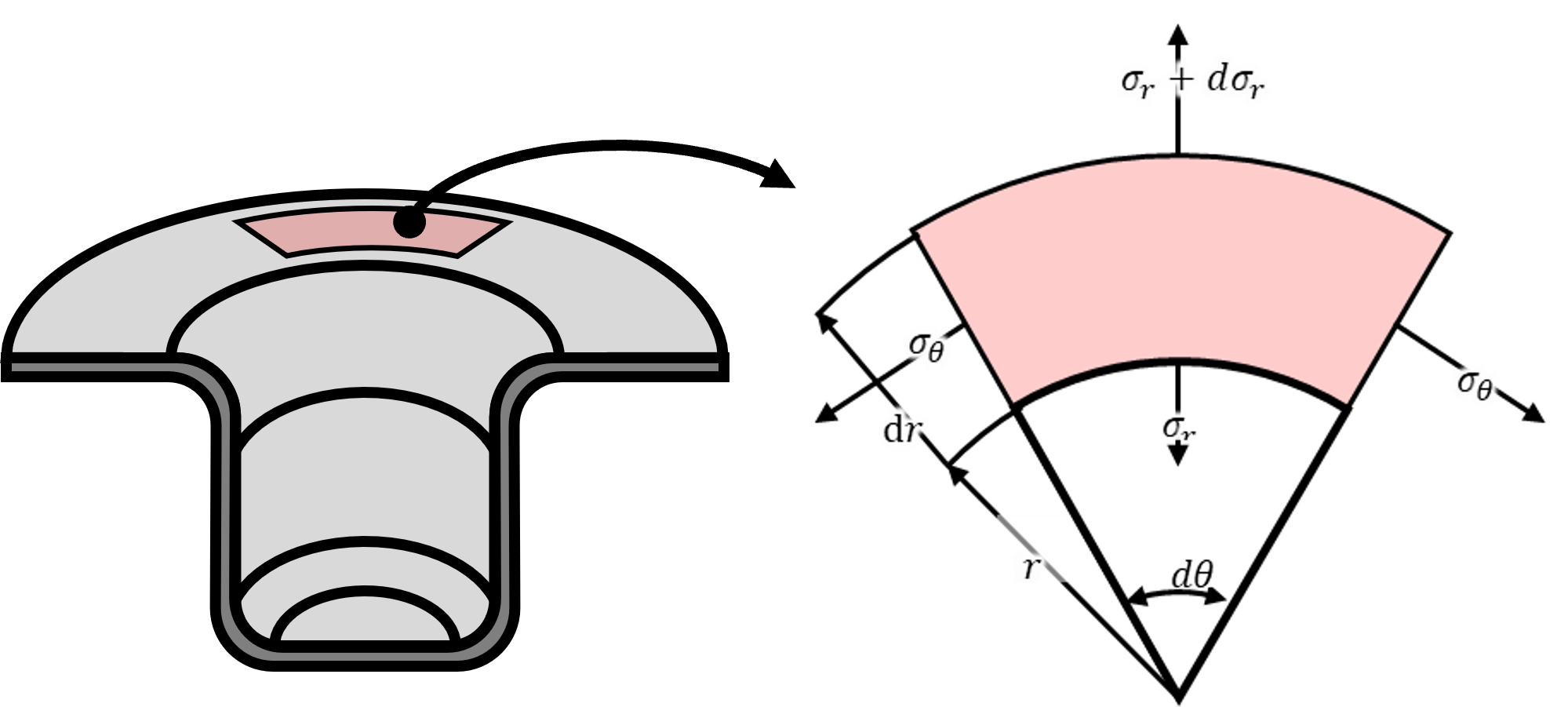
フランジの材料要素の一部を切り出したのが上右図である。 フランジ部はパンチによる絞り成形によって引き込まれるため、円周方向に圧縮応力σ𝜃が発生する。 そしてσ_θと釣り合うために円周の法線方向に引張応力σ_rが発生する。 σ_rとσ_θは以下の式で示すことができる。

なお、降伏応力をσ_Yとする。
またσ_Fは摩擦力によるもので、クッション圧をF_H、素板と工具の摩擦係数がμとすると、以下の式で示せる。

詳細な計算は補足記事参照のこと

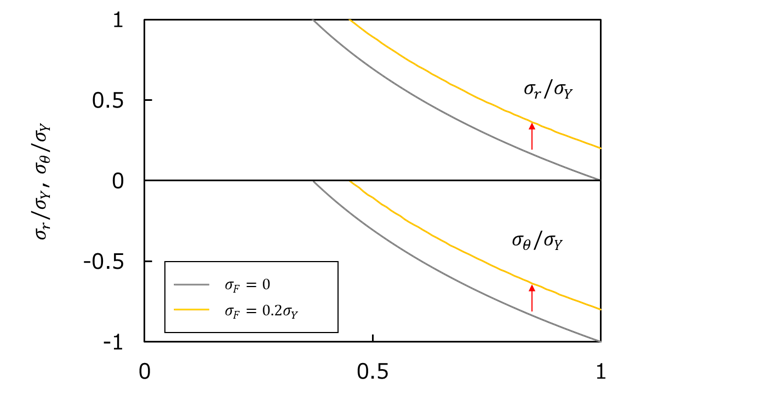
これをグラフにすると上図になる。 なお、グレー線がσ_F=0、黄線がσ_F=0.2σ_Yである。
クッション圧を上げることで、σ_θ/σ_Yが大きくなり0に近づく。 つまり圧縮応力が下がり、シワになりにくくなることがわかる。
一方、クッション圧をあげることで、σ_r/σ_Yも大きくなり1に近づく。 つまり、ワレやすくなることがわかる。
このようにクッション圧は絞り加工に影響を与えることがわかる。

ダイR部の応力計算

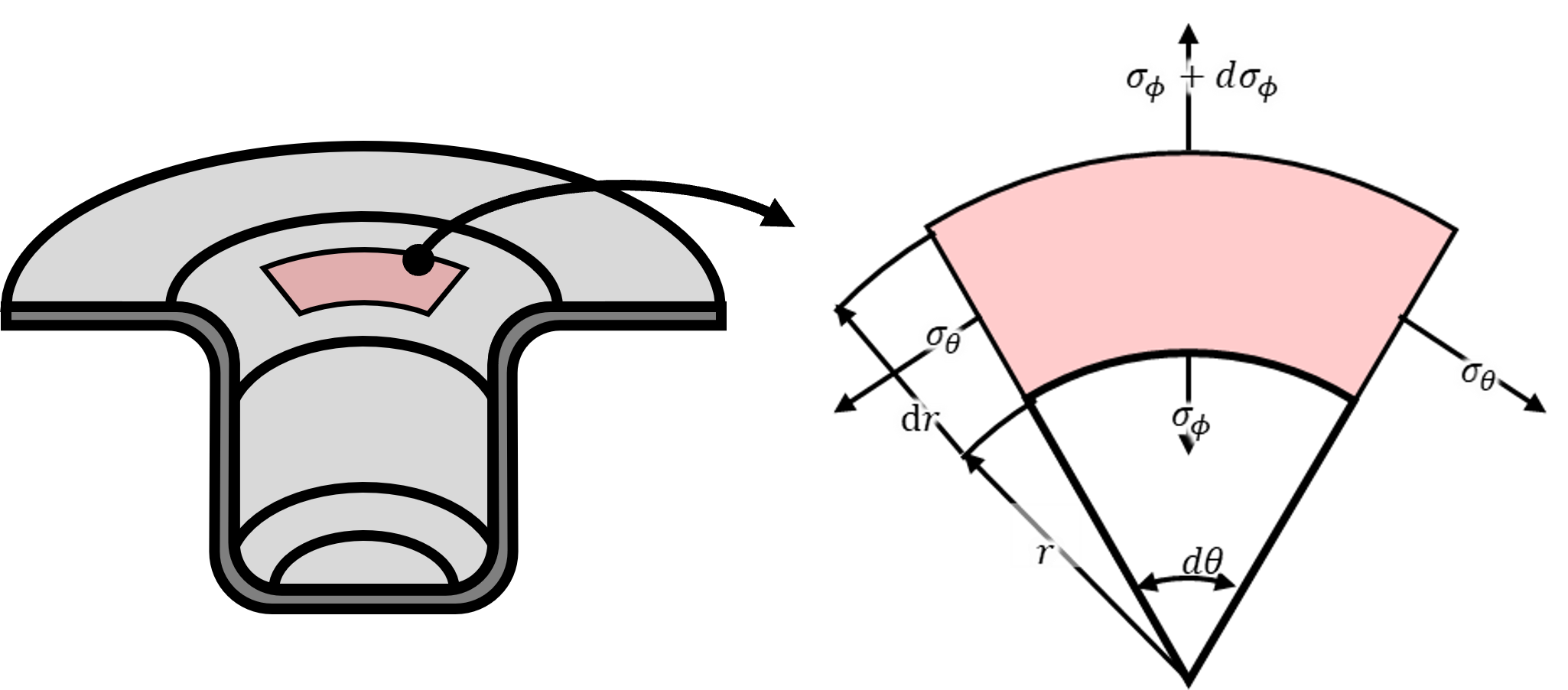
ダイRの材料要素の一部を切り出したのが上右図である。 円周方向の圧縮応力をσ_θ、ダイRの子午線方向の応力をσ_φとする。 ダイRではフランジ部と異なり曲げ応力が発生する。 ただし、式が煩雑になるため、本ページでは板厚変化・摩擦力・曲げの影響を無視する。 （フランジ部では板厚変化は無視していたが、摩擦力を考慮していた） σ_φとσ_θは以下の式で示すことができる。

詳細な計算は補足記事参照のこと

パンチ荷重の計算

上図は再掲にはなるが、円筒絞りの断面図である。
パンチ荷重を計算するためには、側壁部にかかる荷重を求めればよい。
側壁部の面積は直径×板厚なので2πrt
σ_φの加工方向成分はσ_φsinφ
よってパンチ荷重Pは以下の式で示せる。

\[ P=2\pi rt \sigma_\phi sin\phi \]

例えば、D 90mm, d 73mm, r_p,r_d 6.5mm, t 1mm, σ_Y 200MPaとすると以下の様なグラフになる。

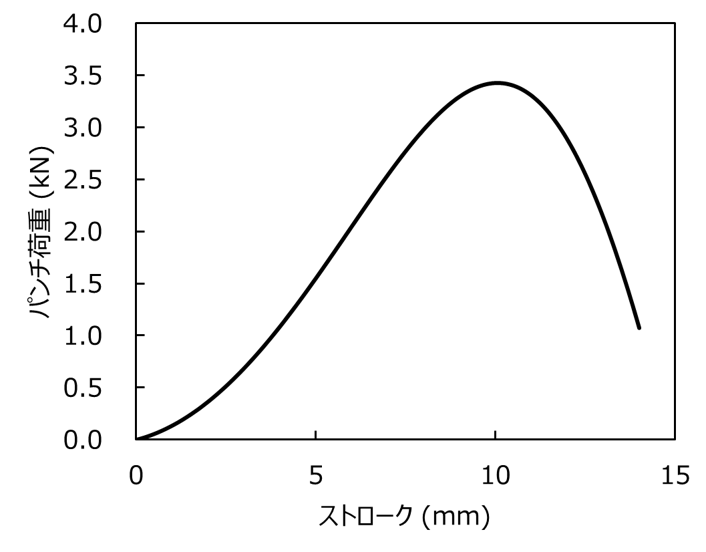
ただし、このやり方で荷重の最大値を手計算で求めるのは困難である。 そこで、簡素化した式で荷重の最大値を求める。

\[ P_{max}=K_1\pi dt \sigma_B \]

K1は、絞り率とブランク材の板厚と直径の比で決められた定数である。 またσ_Bは引張強度である。